Question

Find the 18th term as well as the sum of the 1st twenty three terms of each of the

following arithmetic sequences:
a) 4; 7; 10; …………….
b) -15; -8; -1; …………

Answer 1

Explanation:

a) 4 , 7 , 10 , . . . . .

Here we can see that ,

• Common difference = 10-7 = 3
• First term = 4.

We know the formula of nth term as ,

`\implies T_n = a+(n-1)d\\\\\implies T_(18 )= 4 + (18-1)3 \\\\\implies T_(18) = 4 + 51 \\\\\implies \boxed{ T_(18) = 55 }`

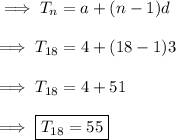
Sum of 20 terms as ,

`\implies S_n = (n)/(2)[2a+(n-1)d] \\\\\implies S_(20) = (20)/(2)[2(4)+(20-1)3] \\\\\implies S_(20) = 10[ 8 + 57 ] \\\\\implies \boxed{ S_(20 )= 650 }`

b) -15 , -8 , -1 . . . . .

Here we can see that ,

• Common difference = -8+15 = 7.
• First term = (-15).

We know the formula of nth term as ,

`\implies T_n = a+(n-1)d\\\\\implies T_(18) = -15 + (18-1)7 \\\\\implies T_(18) = -15+ 119 \\\\\implies \boxed{ T_(18) = 104 }`

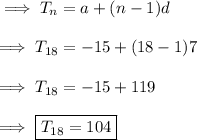
Sum of 20 terms as ,

`\implies S_n = (n)/(2)[2a+(n-1)d] \\\\\implies S_(20) = (20)/(2)[2(-15)+(20-1)7] \\\\\implies S_(20) = 10[ -15+ 133 ] \\\\\implies \boxed{ S_(20) = 1180 }`