Question

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 9.4% per hour.

How many hours does it take for the size of the sample to double?
Note: This is a continuous exponential growth model.
Do not round any intermediate computations, and round your answer to the nearest hundredth.
oo
E

Answer 1

It takes 7.37 hours for the size of the sample to double.

Explanation:

Continuous exponential growth model:

The continuous exponential growth model for populations is given by:

`P(t) = P(0)e^(rt)`

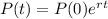
In which P(0) is the initial population and r is the growth rate parameter, as a decimal.

Growth rate parameter of 9.4% per hour.

This means that
`r = 0.094`

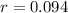
So

`P(t) = P(0)e^(rt)`

`P(t) = P(0)e^(0.094t)`

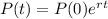
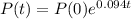
How many hours does it take for the size of the sample to double?

This is t for which P(t) = 2P(0). So

`P(t) = P(0)e^(0.094t)`

`2P(0) = P(0)e^(0.094t)`

`e^(0.094t) = 2`

`\ln{e^(0.094t)} = ln(2)`

`0.094t = ln(2)`

`t = (ln(2))/(0.094)`

`t = 7.37`

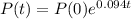
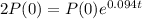
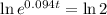
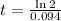
It takes 7.37 hours for the size of the sample to double.