Answer:
The numbers are 19 and 5
Explanation:
Given
Let the numbers be
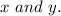
So:
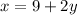 --- First statement
--- First statement
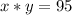 --- second statement
--- second statement
Required
Find x and y
Substitute
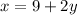 in
in
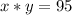
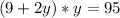
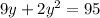
Rewrite as:
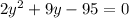
Expand
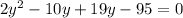
Factorize
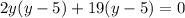
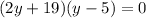
Solve for y
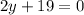 or
or
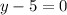
 or
or
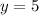
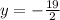 or
or
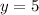
Since the numbers are positive, we take only:
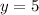
Substitute
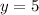 in
in
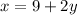
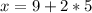
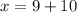
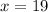
The numbers are 19 and 5