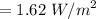Solution :
Given :
Wavelength of the thin beam of light, λ = 50 μm
Distance of the screen from the slit, D = 3.00 m
Width of the fringe, Δy = ±8.24 mm
Therefore, width of the slit is given by :
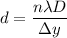
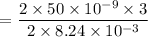
= 0.000018203 m
= 0.0182 mm
= 0.018 mm
The intensity of light is given by :
 , where
, where
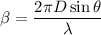
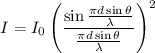
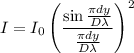
Now,

= 0.1854
≈ 0.18
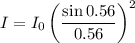
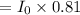
= 2 x0.81