Question

1) Solve.

Manny invested $1,200 at a simple interest rate of5%(0.05). How much money would he have after 7 years?


2)Solve.

Approximately how much money would Manny have if he invested $1,200 at an interest rate of 5% for 7 years compounded monthly (12 times a year)?


3) Solve.

If the value of a stock depreciates at 3% a year, what will a $100 investment be worth in 20 years?


4) Solve.

Iodine-131 has a half-life of 8 days. How much would be left of an original 40g sample after 40 days?


5) Use elimination to find the answer, and then choose the correct answer.

A restaurant is offering a special deal on pizza and drinks. You can get 2 large pizzas and 4 large drinks for $16. Or, you can get 4 large pizzas and 7 large drinks for $30. How much would each pizza (p) and each drink (d) cost separately?

Answer 1

Explanation:

1. Given : P = $1200 , R = 5%, T = 7 years

Therefore, the simple interest is,
`$SI = (PTR)/(100)$`

`$=(1200 * 7 * 5)/(100)$`

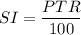
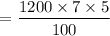
= $ 420

Therefore, total amount Manny will have is A = P + Si

= 1200 +420

= $ 1620

2. Given : P = $1200 , r = 5%, t = 7 years, n = 12 times (compounded)

So the amount is :

`A=P\left(1+(r)/(n)\right)^(nt)`

`A=1200\left(1+(0.05)/(12)\right)^(12* 7)`

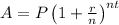
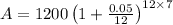
= 1692.17

So Manny would have approximately $ 1692 when compounded monthly.

3. Given :

The amount of stock = $ 100

rate of depreciation = 3%

Time = 20 years.

Therefore, using compound interest, we get

Future value = initial value x
`$(1-\text{rate})^(number of years)$`

=
`$100 * (1 - 3 \%)^(20)$`

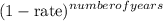
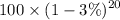
= 54.38

So after 20 years, the value would be $ 54.38

4. Given :

Initial amount, i = 40 gram

time, t = 40 days

half life of the isotope, h = 8 days

1/2 is used because of half life

Therefore, the final amount is given by :

`$a=i * \left((1)/(2)\right)^(t/h)$`

`$a=40* \left((1)/(2)\right)^(40/8)$`

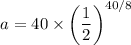
= 1.25 gram

So after 40 days, 1.25 gram will be left.

5. Let p = pizza and d = drink

So according to the question,

2p + 4d = $ 15 ....(i)

4p + 7d = $ 30...(ii)

Equation equation (i) and (ii), we get

d = $0

and p = $ 7.5