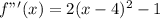The parent function of a quadratic equation is vertically stretched by a factor of 2, then translated 4 units left and one unit down

Question

asked Mar 12, 2022 33.7k views

1 Answer

Vladli · Answer 1 · 2022-03-16T09:00:03+0000

Answer:

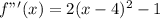
Explanation:

Given

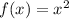f(x) = x^2 --- the quadratic function

Vertically stretched by 2

Translation:
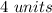$4\ units$ left and
$1\ unit$ down

Required

Determine the new function

f(x) = x^2

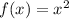
The rule for vertical stretch is:

$(x,y) \to (x,ay)$

In this case:

a = 2

So, we have:

f(x) = x^2

f'(x) = a * f(x)

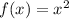
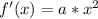
f'(x) = a * x^2

Substitute:
a = 2

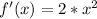
f'(x) = 2 * x^2

f'(x) =2x^2

Translation: 4 units left

The rule is:

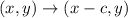
$(x,y) \to (x - c,y)$

In this case:
c =4

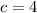
So, we have:

Translation: 1 unit down

The rule is:

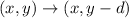
$(x,y) \to (x,y-d)$

In this case,
d=1

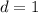
So, we have: