Answer:
a) The angular speed of the combination is 0.667 radians per second (clockwise).
b) 98.829 per cent is lost due to friction.
Step-by-step explanation:
a) Since no external load applied on any of the cylinders before, during and after the coupling, angular momentum of the entire system is constant. In consequence, we apply the Principle of Angular Momentum Conservation to calculate the final angular speed of the combination:
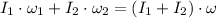 (1)
(1)
Where:
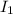 - Moment of inertia of the first cylinder, in kilogram-square meters.
- Moment of inertia of the first cylinder, in kilogram-square meters.
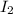 - Moment of inertia of the second cylinder, in kilogram-square meters.
- Moment of inertia of the second cylinder, in kilogram-square meters.
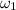 ,
,
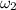 - Initial angular speeds of the first and second cylinder, in radians per second.
- Initial angular speeds of the first and second cylinder, in radians per second.
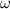 - Final angular speed of the entire system, in radians per second.
- Final angular speed of the entire system, in radians per second.
If we know that
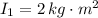 ,
,
 ,
,
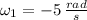 and
and
 , then the final angular speed of the entire system is:
, then the final angular speed of the entire system is:

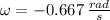
The angular speed of the combination is 0.667 radians per second (clockwise).
b) By Principle of Energy Conservation and Work-Energy Theorem, the energy lost due to friction (
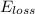 ), in joules, is equal to the change in the total kinetic energy of the system. Given that both cylinder have pure rotation, kinetic energy is due to only rotation. That is:
), in joules, is equal to the change in the total kinetic energy of the system. Given that both cylinder have pure rotation, kinetic energy is due to only rotation. That is:
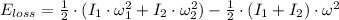 (2)
(2)
If we know that
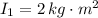 ,
,
 ,
,
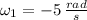 ,
,
 and
and
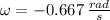 , then the energy lost due to friction is:
, then the energy lost due to friction is:
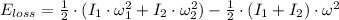
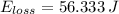
The original amount of kinetic energy (
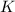 ), in joules, is:
), in joules, is:
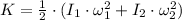

Lastly, the percentage of the original kinetic energy lost to friction is:
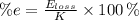
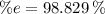
98.829 per cent is lost due to friction.