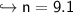Answer:
she should save it for minimum 9.1 years.
Step-by-step explanation:
- compound interest formula:

- where A is money earned, P is investing money, r is rate of interest, n is time.
solve:

change sides

take ln on both sides
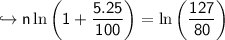
simplify
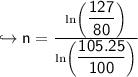
final answer
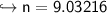
rounding to nearest tenth