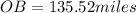Question

A helicopter flies from the airport on a course with a bearing of 21 degrees. After flying for 99 ​miles, the helicopter flies due east for some time. The helicopter flies back to the airport with a bearing of 227 degrees. How far did the helicopter fly on the final leg of its​ journey?

Answer 1

Explanation:

From the question we are told that:

Initial bearing
`\angle _1=21 \textdegree`

Initial distance
`d_1=99miles`

Final bearing
`\angle _2=227 \textdegree`

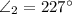
Let
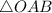`\triangle OAB` be the perimeter travailed

`\angle OAB=90+21=111 \textdegree\\\angle ABO=270-227=43 \textdegree`

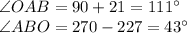
Generally the equation for OB using sine rule is mathematically given by

`OB=99*(sin111)/(sin43)`

`OB=135.52miles`

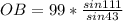
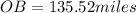
Therefore the helicopter flight on the final leg of its​ journey is

`OB=135.52miles`