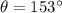Question

A plane is flying with an airspeed of 190 miles per hour and heading 150°. The wind currents are running at 30 miles per hour at 170° clockwise from due north. Use vectors to find the true course and ground speed of the plane. (Round your answers to the nearest ten for the speed and to the nearest whole number for the angle.)

Answer 1

`Vg=200mile/hr`

`\theta=153 \textdegree`

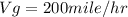
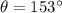
Step-by-step explanation:

From the question we are told that:

Plane airspeed
`v_p=190mil/h`

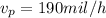
Plane direction
`\angle=150 \textdegree`

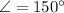
Wind current speed
`V_w=30mil/h`

Wind direction
`\angle=150 \textdegree`

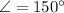
Generally the vector form of the forces is mathematically given by

For plane

`\angle Q_p=90-150 \textdegree`

`V_p=170(cos60 \textdegree ,sin60 \textdegree)`

`V_p=(85,-147.224)`

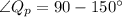
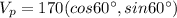
For wind

`\angle Q_w=90-170 \textdegree`

`V_w=30(cos-80 \textdegree ,sin-80 \textdegree)`

`V_w=(5.2,-29.54)`

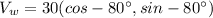
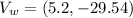
Generally the equation for resultant force is mathematically given by

`v_r=V_a+V_w`

`v_r=(85,-147.224)+(5.2,-29.54)`

`v_r=(90.21,-176.76)`

`v_r=198.45\angle -63`

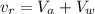
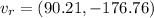
Therefore ground speed

`V_g=198.5miles/hr`

`Vg=200mile/hr`

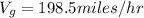
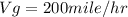
Direction

`\theta=(90+63)=153 \textdegree`

`\theta=153 \textdegree`