Question:-
If the radius of the base of the cone, r, is
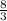 units and the height, h, is 13 units, what is the volume of the cone ?
units and the height, h, is 13 units, what is the volume of the cone ?
Answer:-
Given:-
 Radius of the base of the cone (r) is
Radius of the base of the cone (r) is
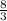 units.
units.
 Height (h) of the cone is 13 units.
Height (h) of the cone is 13 units.
To Find:-
Volume of the cone.
Solution:-
We know,
Formula of volume of cone is
 πr²h
πr²h
So, volume of the cone =
 ×
×
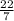 ×
×
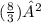 × 13
× 13
=
 ×
×
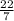 ×
×
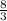 ×
×
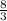 × 13
× 13
=
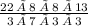
=
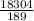
= 96.85 cubic units.
Volume of the cone is 96.85 cubic units. [Answer]