Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.(Quadratic Word Problems (Profit/Gravity)

y=-16x^2+121x+83

Answer 1

The rocket will hit the ground after about 8.20 seconds.

Explanation:

The height of the rocket y, in feet, x seconds after launch is modeled by the equation:

`y=-16x^2+121x+83`

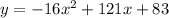
We want to find the time at which the rocket will hit the ground.

If it hits the ground, the height of the rocket y will be 0. Thus:

`0=-16x^2+121x+83`

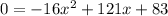
We can solve for x. Factoring (if possible at all) or completing the square can be tedious, so we can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

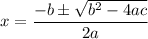
In this case, a = -16, b = 121, and c = 83. Substitute:

`\displaystyle x=(-(121)\pm√((121)^2-4(-16)(83)))/(2(-16))`

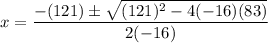
Simplify:

`\displaystyle x=(-121\pm√(19953))/(-32)`

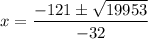
Divide everything by -1 and simplify the square root. The plus/minus will remain unchanged:

`\displaystyle x=(121\pm3√(2217))/(32)`

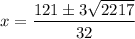
Therefore, our two solutions are:

`\displaystyle x=(121+3√(2217))/(32)\approx 8.20\text{ or } x=(121-3√(2217))/(32)\approx -0.63`

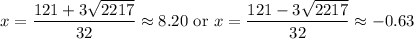
Since time cannot be negative, we can ignore the second solution.

Therefore, the rocket will hit the ground after about 8.20 seconds.