Answer:
Yes
Explanation:
Given
GH:
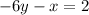
Required
Can EF be

First, we determine the slope of GH
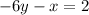
Solve for 6y

Solve for y
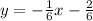
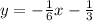
An equation has the form:
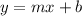
Where
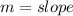
By comparison:
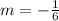
Next, determine the slope of EF

Make y the subject
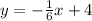
The slope is:
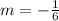
Compare the slopes of both lines.
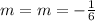
Since they have the same slopes, then the equation of EF is possible