Question

Help pls. Show your work!!

Answer 1

True

Explanation:

given
`f(x)=\sqrt[4]{2x-6}` and
`g(x)=(1)/(2) x^(4)+3`

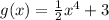
to find the inverse we just switch the x and y values for one of the functions,

in this case I will chose f(x) [note f(x) is just another way of saying y]

`x=\sqrt[4]{2y-6}`

solve for x;

raise both sides to the 4th power

`x^(4)=2y-6`

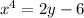
add 6 to both sides

`x^(4) +6=2y-6-6\\=x^(4)+6=2y`

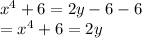
divide both sides by 2 and you get

`(x^(4) +6)/(2) =(2)/(2) y`

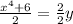
simplify and you get

`y=(1)/(2) x^(4) +3`

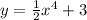
which equals to g(x).

hope this helps, for practice, I would recommend you switch the x and y of g(x)