Answer:
The possible coordinates of point A are
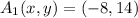 and
and
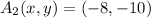 , respectively.
, respectively.
Explanation:
From Analytical Geometry, we have the Equation of the Distance of a Line Segment between two points:
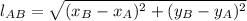 (1)
(1)
Where:
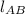 - Length of the line segment AB.
- Length of the line segment AB.
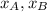 - x-coordinates of points A and B.
- x-coordinates of points A and B.
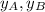 - y-coordinates of points A and B.
- y-coordinates of points A and B.
If we know that
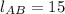 ,
,
 ,
,
 and
and
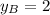 , then the possible coordinates of point A is:
, then the possible coordinates of point A is:
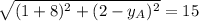
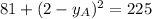
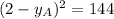
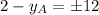
There are two possible solutions:
1)
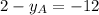
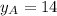
2)
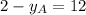
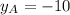
The possible coordinates of point A are
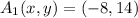 and
and
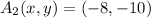 , respectively.
, respectively.