Answer:
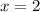 ;
;
 and
and

Explanation:
Given
Let the sides of the cuboid be: x, y and z
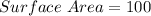
Required
Find x, y and z
The surface area is calculated as:
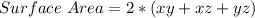
Substitute
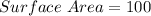
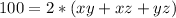
Divide both sides by 2
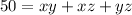
Rewrite as:

Now, we use trial by error method to determine the values of x, y and z.
Let
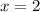 and
and

Solve for z:
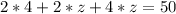
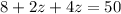
Collect like terms
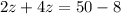
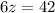
Divide both sides by 6


So, we have:
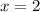 ;
;
 and
and

The above values are all integers;
Hence, it is possible to determine a cuboid with the stated requirement