Question

A line passes through the point (-5,-1) and has a slope of 4

write an equation in slope intercept form for this line

Answer 1

`\displaystyle y = 4x + 19`

Step-by-step Step-by-step explanation:

Plug the information into the Slope-Intercept Formula like so:

`\displaystyle y = mx + b \\ \\ -1 = 4[-5] + b \hookrightarrow -1 = -20 + b; 19 = b \\ \\ \\ \boxed{y = 4x + 19}`

I am joyous to assist you at any time.

Answer 2

Hello.

We have a point that the line passes through:

`\mathrm{(-5,-1)}`

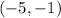
We also have the line's slope:

`\mathrm{4}`

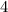
Right now, we do not have enough information to write the equation of the line in slope-intercept form. We need to know the slope and the y-intercept. We do know the slope, but we do not know the y-intercept...yet.

We do have enough information to write the line's equation in Point-Slope Form:

`\mathrm{y-y1=m(x-x1)}`

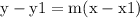
Plug in the values:

`\mathrm{y-(-1)=4(x-(-5)}`

`\mathrm{y+1=4(x+5)}`

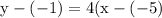
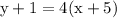
Use the Distributive Property (a(b+c)=ab+ac) :

`\mathrm{y+1=4x+20}`

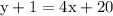
Move 1 to the right:

`\mathrm{y=4x+20-1}`

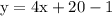
Subtract:

`\mathrm{y=4x+19}`

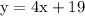
Now we have the equation in slope-intercept form.

Therefore, the answer is

`\mathrm{y=4x+19}`

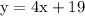
I hope it helps.

Have a nice day.

`\boxed{imperturbability}`