Answer:
see explanation
Explanation:
The equation of a circle centred at the origin is
x² + y² = r² ( r is the radius )
x² + y² = 16 ← is the equation of a circle
centre (0, 0 ) and r =
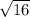 = 4
= 4
The circle therefore intercepts the x- axis at (4, 0 ) and (4, 0 )
and intercepts the y- axis at (0, - 4 ) and (0, 4 )
Domain is - 4 ≤ x ≤ 4
range is - 4 ≤ y ≤ 4
x- intercepts are x = - 4, x = 4
y- intercepts are - 4, 4