Answer:
a) 52.915 m
b) The vertical velocity is approximately 21.092 m/s
The resultant velocity is approximately 26.5 m/s
Step-by-step explanation:
a) The height of the window in the house from which the water was thrown = 15 m
The speed of the stream of water thrown = 20 m/s
The angle at which the water was thrown = 37° over the horizontal
The acceleration due to gravity, g = 10 m/s²
a) The distance from the base of the house at which the water will fall is given as follows;
y = y₀ + u·t·sin(θ) + 1/2·g·t²
Where;
y = The vertical height reached
u = The initial velocity
t = Time of flight
From the point the steam of water is thrown, we get;
y₀ = 15 m
Therefore;
y = 15 + 20 × t × sin(37°) - 1/2 × 10 × t²
y = 15 + 20 × t × sin(37°) - 5 × t²
When y = 0, Ground level, we get
0 = 15 + 20 × t × sin(37°) - 5 × t²
5·t² - 20×sin(37°)×t -15 = 0
∴ t = (20 ×sin(37°) ± √((-20 × ·sin(37°))² - 4 × (5) × (-15)))/(2 × 5)
t ≈ 3.3128302, or t ≈ 0.906
Therefore, the time of flight of the water, t ≈ 3.3128302 seconds
The distance from the base of the house at which the water will fall = The horizontal distance travelled by the water, x
x = u·cos(θ)×t
∴ x = 20 × cos(37°) × 3.3128302 ≈ 52.915
The distance from the base of the house at which the water will fall = x ≈ 52.915 m
b) The velocity at which the water will reach the ground, 'v', is given as follows;
The vertical velocity,
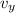= u·sin(θ)·t - g·t
At the ground, t ≈ 3.3128302 seconds
∴
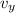= 20 × sin(37) - 10 × 3.3128302 ≈ -21.092
The vertical velocity at which the water will reach the ground,
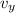≈ 21.092 m/s (downwards)
The resultant velocity, v = √(
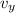² + vₓ²)
∴ v = √(21.092² + (0 × cos(37°))²) ≈ 26.5
The resultant velocity at which the water will reach the ground, v ≈ 26.5 m/s.