Question

Which of the following measurements could be the side lengths of a right triangle?

Answer 1

Option A

Explanation:

Here we need to tell which could be the side lengths of a right angled triangle . As we know that in a right angled triangle , the sum of square two sides along the right angle is equal to the square of side opposite to right angle .

That is ,

`\longrightarrow a^2 = b^2+ c^2`

`\begin{picture}(8,8)\setlength{\unitlength}{1cm} \thicklines\put(0,0){\line(1,0){4}}\put(4,0){\line(0,1){3}}\put(4,3){\line(-4,-3){4}}\put(2,-0.5){$\sf √(48)in$}\put(4.4,1.5){$\sf √(12)in. $} \put(1.2,2){$\sf √(60)in. $}\end{picture}`

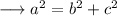
We can start by looking at the options , first option is ,

`\longrightarrow √(48)\ in , √(12)\ in , √(60) in`

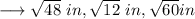
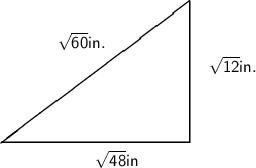
So by squaring first two sides and adding them , we have ,

`\longrightarrow (√(48))^2+(√(12))^2\\`

`\longrightarrow 48+12 = 60`

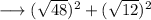
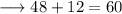
And by squaring the third side we have ,

`\longrightarrow √(60)^2 = 60`

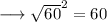
Hence here the sum of square of two sides is equal to the square of third side .

Therfore the triangle with sides √48 in , √12in and √60 forms a right angle ∆.