Answer:
The remaining side and angles are
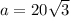 ,
,
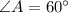 and
and
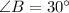 .
.
Explanation:
According to the information given on statement, we are in front of a right triangle because
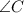 , opossite to side
, opossite to side
 , is a right angle. Hence,
, is a right angle. Hence,
 is the hypotenuse of the right triangle and
is the hypotenuse of the right triangle and
 , a leg. The missing length can be calculated by the Pythagorean Theorem:
, a leg. The missing length can be calculated by the Pythagorean Theorem:
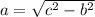 (1)
(1)
If we know that
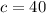 and
and
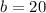 , then the length of the missing leg is:
, then the length of the missing leg is:
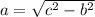
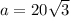
Lastly, we find the value of the missing angles by means of direct and inverse trigonometric relations:
Angle A
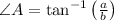 (2)
(2)
Angle B
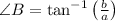 (3)
(3)
If we know that
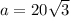 and
and
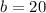 , then the values of the missing angles are, respectively:
, then the values of the missing angles are, respectively:
Angle A
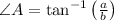
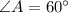
Angle B
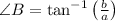
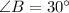
The remaining side and angles are
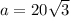 ,
,
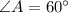 and
and
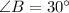 .
.