Question

Evaluate 1/3b+7/12 when b= 1/4 .

Answer 1

`(23)/(12)`

Alternative forms:

`1.916, 1(11)/(12)`

Explanation:

Substitute b = 1/4 into 1/3b + 7/12 :

`\begin{matrix}\underline{1}\\\underline{3}\\4\\\end{matrix}+(7)/(12)`

Calculate

`\begin{matrix}\underline{1}\\\underline{3}\\4\\\end{matrix}+(7)/(12)`

Divide a fraction by multiplying its reciprocal

`(4)/(3)+(7)/(12)`

Find common denominator and write the numerators above common denominator

`(4*4)/(3*4)+(7)/(12)`

Calculate the product or quotient

`(16)/(3*4)+(7)/(12)`

`(16+7)/(12)`

Calculate the sum or difference

`(23)/(12)`

I hope this helps you

:)

Answer 2

`(2)/(3)`

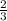
Explanation:

Since we know that
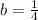`b=(1)/(4)`, we can simply substitute
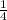`(1)/(4)` for
`b` in the equation:

`(1)/(3)b+(7)/(12)\\(1)/(3)((1)/(4))+(7)/(12)\\`

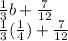
To multiply fractions, simply multiply the numerators of the multipliers to find the numerator of the resultant, and multiply the denominators of the multipliers to find the denominator of the resultant. Therefore, we multiply 1 x 1, which is 1, and 3 x 4, which is 12. The resultant fraction for the operation of
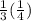`(1)/(3)((1)/(4))` is
`(1)/(12)`.

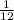Now, we just need to add the remaining fractions:

`(1)/(12)+(7)/(12)`

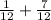
When adding fractions with the sane denominator, we simply add the numerators. The addition of the numerators in this case is 8, so:

`(1)/(12)+(7)/(12)=(8)/(12)`

We can still simplify the fraction of
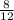`(8)/(12)`. Both the numerator and the denominator are divisible by four, so divide them both by four to get the final, simplified fraction:

`(8)/(12)=(2)/(3)`