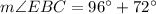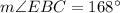Answer:
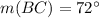
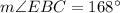
Explanation:
Given
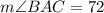
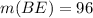
See attachment for circle
Required
Determine
(a) Measure of BC
(b) Measure of EBC
(a) Measure of BC
From the attachment, we can see that:
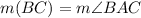 because they belong to the same sector
because they belong to the same sector
This gives:
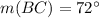
(b) Measure of EBC
From the attachment, we can see that:
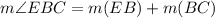
Where
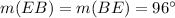
So, we have: