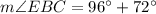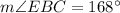Question

I’m circle a shown, secant de and tangent dg are drawn. It is known that angle bac equals 72 degrees and arc be equals 96 degrees

Answer 1

`m(BC) = 72^\circ`

`m\angle EBC = 168^\circ`

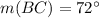
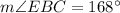
Explanation:

Given

`m\angle BAC = 72`

`m(BE) = 96`

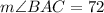
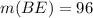
See attachment for circle

Required

Determine

(a) Measure of BC

(b) Measure of EBC

(a) Measure of BC

From the attachment, we can see that:

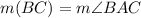`m(BC) = m\angle BAC` because they belong to the same sector

This gives:

`m(BC) = 72^\circ`

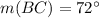
(b) Measure of EBC

From the attachment, we can see that:

`m\angle EBC = m(EB) +m(BC)`

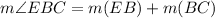
Where

`m(EB) = m(BE) =96^\circ`

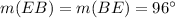
So, we have:

`m\angle EBC = 96^\circ + 72^\circ`

`m\angle EBC = 168^\circ`