Question

The small piston of the hydraulic press with an area of 20 cm² is subjected to a force of 200 N and has lowered by 50 cm. What force acts on a large piston with an area of 0.01 m² and to what height did it rise? (I already found out that large piston force is 1000N how do I calculate in what height did it rise?)

Answer 1

The large piston would rise by
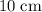`10\; \rm cm` (which is equal to
`0.1\; \rm m`.)

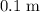Step-by-step explanation:

Convert the unit of the area of the larger piston to
`\rm cm^(2)`:

`0.01\; \rm m^(2) = 100\; \rm cm^(2)`.

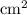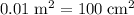If the pipe is cylindrical, the liquid that the smaller piston pushed into the pipe would be a cylinder:

• Height of the cylinder:
  `50\; \rm cm`.
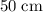• Area of the top of the cylinder:
  `20\; \rm cm^(2)` (same as the area of the smaller piston.)

Volume of liquid that the smaller piston pushed into the pipe:

`\begin{aligned} & \text{Volume of Cylinder} \\ &= \text{Area of the Top of the Cylinder} \\ &\quad\quad * \text{Height of Cylinder} \\ &= 20\; \rm cm^(2) * 50\; \rm cm \\ &= 1000\; \rm cm^(3) \end{aligned}`.

Unlike gas, the volume of a liquid (such as the one in this hydraulic press) at a given temperature tends to be fixed.

Therefore, when the small piston pushed
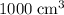`1000\; \rm cm^(3)` of liquid into the pipe, liquid of the exact same volume (
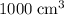`1000\; \rm cm^(3)\!`) would appear under the larger piston and push the larger piston upwards.

Rearrange the equation to find the height by which the larger piston rises (same as the height of the
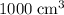`1000\; \rm cm^(3)` liquid cylinder under the larger piston.)

`\begin{aligned} & \text{Height of Cylinder} \\ &= \frac{\text{Volume of the Cylinder}}{\text{Area of the Top of the Cylinder}} \\ &= (1000\; \rm cm^(3))/(100\; \rm cm^(2)) = 10\; \rm cm \end{aligned}`.