Answer:
The calculated value Z = 1.548 < 2.326 at 0.01 level of significance
The Null Hypothesis is accepted
There is no change in the weekly production
Explanation:
Step(i):-
Given that the mean Population(μ) = 200
Given that the standard deviation of the Population(σ) =16
Given that the mean of the sample (x⁻) = 203.5
Given that the size of the sample(n) = 50
Level of significance = 0.01
Critical value Z₀.₀₁ = 2.326
Null hypothesis : (μ) = 200
Alternative Hypothesis : (μ) ≠200
Step(ii):-
Let 'X' be a random variable in a normal distribution
Test statistic

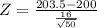
Z = 1.548
The calculated value Z = 1.548 < 2.326 at 0.01 level of significance
The Null Hypothesis is accepted
Final answer:-
There is no change in the weekly production