Question

Urgently plsss A randomly generated password contains four characters. Each of the four characters is either a lowercase letter or a digit from 0–9. Each character in the password cannot be used more than once.

What is the approximate probability that exactly one of the four characters will be a number?

1%
11%
28%
44%

Answer 1

28%

Explanation:

Trust me, it is not 44%

Answer 2

44%

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the values are is important(0123 is a different password of 3210), which means that the permutations formula is used to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

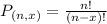
Desired outcomes:

One number, from a set of 10

Three characters, from a set of 26.

They can be in 4 possible orders(CNNN, NCNN, NNCN, NNNC). So

`D = 4P_(10,1)P_(26,3) = 4*(10!)/((10-9)!)*(26!)/((26-3)!) = 624000`

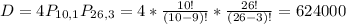
Total outcomes:

Four characters, from a set of 26 + 10 = 36. So

`T = P_(36,4) = (36!)/((36-4)!) = 1413720`

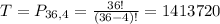
What is the approximate probability that exactly one of the four characters will be a number?

`P = (D)/(T) = (624000)/(1413720) = 0.4414`

So 44%.