Answer:
1)
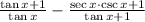 Given
Given
2)
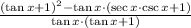
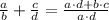
3)
![(\left((\sin x)/(\cos x) + 1 \right)^(2)-\left((\sin x)/(\cos x) \right)\cdot \left[\left((1)/(\cos x) \right)\cdot \left((1)/(\sin x) \right) + 1\right])/(\left((\sin x)/(\cos x) \right)\cdot \left((\sin x)/(\cos x) +1\right))](https://img.qammunity.org/2022/formulas/mathematics/high-school/g2xtt9i61su6d76mh8r49f0ss259q9xra0.png) Identities for tangent, secant and cosecant functions.
Identities for tangent, secant and cosecant functions.
4)
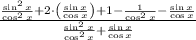 Distributive property/
Distributive property/
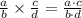
5)
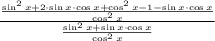
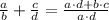
6)
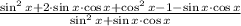
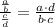
7)
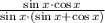 Fundamental trigonometric identity/Existence of additive inverse/Modulative property/Distributive property
Fundamental trigonometric identity/Existence of additive inverse/Modulative property/Distributive property
8)
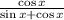 Associative property/Existence of multiplicative inverse/Modulative property/Result.
Associative property/Existence of multiplicative inverse/Modulative property/Result.
Explanation:
Now we proceed to demonstrate by algebraic and trigonometric means the following trigonometric identity:
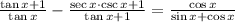
1)
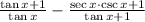 Given
Given
2)
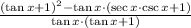
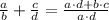
3)
![(\left((\sin x)/(\cos x) + 1 \right)^(2)-\left((\sin x)/(\cos x) \right)\cdot \left[\left((1)/(\cos x) \right)\cdot \left((1)/(\sin x) \right) + 1\right])/(\left((\sin x)/(\cos x) \right)\cdot \left((\sin x)/(\cos x) +1\right))](https://img.qammunity.org/2022/formulas/mathematics/high-school/g2xtt9i61su6d76mh8r49f0ss259q9xra0.png) Identities for tangent, secant and cosecant functions.
Identities for tangent, secant and cosecant functions.
4)
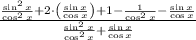 Distributive property/
Distributive property/
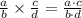
5)
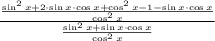
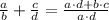
6)
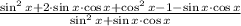
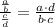
7)
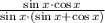 Fundamental trigonometric identity/Existence of additive inverse/Modulative property/Distributive property
Fundamental trigonometric identity/Existence of additive inverse/Modulative property/Distributive property
8)
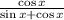 Associative property/Existence of multiplicative inverse/Modulative property/Result.
Associative property/Existence of multiplicative inverse/Modulative property/Result.