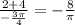Answer:

Explanation:
Use slope formula.
Rise over run.
Or
y over x.
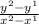
Over changes in x value would be - 3/4 pi.
Plug in seepage intervals for x to find y.
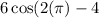
In the regular function,

Since our period is 2, it would stay the same since 1x2=2
Since our amplitude is 6, our y value now is 6.
Since our vertical shift is -4, our y value is 2.
So
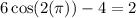

Let do the other point,
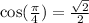
Our period is 2 so
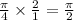
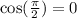
Multiply this by 6.
It stays 0 then subtract 4 we get
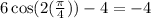
Use the earlier formula, slope