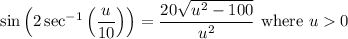Question

Write each expression as an algebraic​ (nontrigonometric) expression in​ u, u > 0.

sin(2sec^-1 u/10)

Answer 1

`\displaystyle \sin\left(2\sec^(-1)\left((u)/(10)\right)\right)=(20√(u^2-100))/(u^2)\text{ where } u>0`

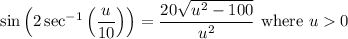
Explanation:

We want to write the trignometric expression:

`\displaystyle \sin\left(2\sec^(-1)\left((u)/(10)\right)\right)\text{ where } u>0`

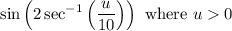
As an algebraic equation.

First, we can focus on the inner expression. Let θ equal the expression:

`\displaystyle \theta=\sec^(-1)\left((u)/(10)\right)`

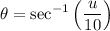
Take the secant of both sides:

`\displaystyle \sec(\theta)=(u)/(10)`

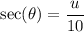
Since secant is the ratio of the hypotenuse side to the adjacent side, this means that the opposite side is:

`\displaystyle o=√(u^2-10^2)=√(u^2-100)`

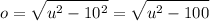
By substitutition:

`\displaystyle= \sin(2\theta)`

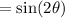
Using an double-angle identity:

`=2\sin(\theta)\cos(\theta)`

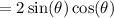
We know that the opposite side is √(u² -100), the adjacent side is 10, and the hypotenuse is u. Therefore:

`\displaystyle =2\left((√(u^2-100))/(u)\right)\left((10)/(u)\right)`

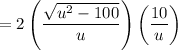
Simplify. Therefore:

`\displaystyle \sin\left(2\sec^(-1)\left((u)/(10)\right)\right)=(20√(u^2-100))/(u^2)\text{ where } u>0`