Answer:
(a)
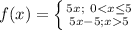
(b) Rate = 5
(c) Rate = 5
Explanation:
Given
The attached graph
Solving (a): The piece-wise function
For the first line
Calculate the slope of the first line

Where
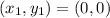
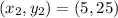
So, the slope is:
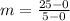
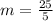

The equation is then calculated as:

Where:
 and
and
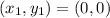
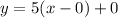

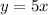
So, the function of the first line is:
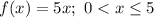
For the second line
Calculate the slope of the second line

Where

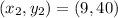
So, the slope is:
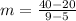
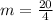

The equation is then calculated as:

Where:
 and
and

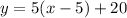
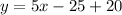
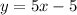
So, the function of the second line is:
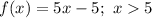
Hence, the piece-wise function is:
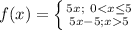
Solving (b): The rate at which customers that buy up to 5lb buy.
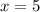
This question implies that, we determine the rate at which this customer buys.
For
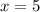
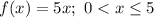
The slope of the above function is 5.
So, this customer buys at the rate of $5 per lb
Solving (b): The rate at which customers that buy more than 5lb buy the extra pounds above 5lb.
For
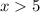
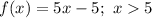
Assume x = 6
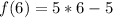
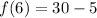
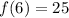
Express as 20 + 5
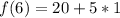
Assume x = 7
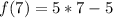
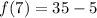
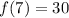
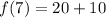
Express 10 as 5 * 2
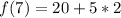
So, we have:
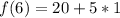
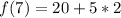
This can be generalized as:
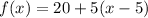
For the above functions;
20 represents the amount they buy the first 5
5 represents the rate at which they buy extra pounds above 5
Hence, they buy the extra pounds at the rate of $5 per pound