Question

A computer processes jobs on a first-come, first served basis in a time-sharing environment. The jobs have Poisson arrival rates average 0.6 jobs per minute. The objective in processing these jobs is that they spend no more than 5 minutes, on average, in the system. Assuming exponential service times, how fast does the computer have to process jobs (in minutes), on average, to meet this objective

Answer 1

0.8 minutes

Explanation:

From the given information:

The arrival time for the jobs to the computer obeys a Poisson distribution;

Thus, the arrival rate is:

`\lambda = 0.6 \ jobs \ per \ minute`

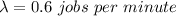
Assuming the average time spent on the jobs in the system is denoted by:

`W_s= 5 \ minutes`

The average time a job process in the system can be expressed as follows:

`W_s = (1)/(\mu - \lambda)`

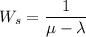
From above formula:

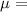`\mu =` service rate

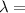`\lambda =` arrival rate

replacing the values;

`5 = (1)/(\mu - 0.6)`

`5(\mu - 0.6) = 1`

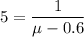
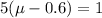
Open brackets

`5 \mu - 3 = 1`

`5 \mu = 3+ 1 \\ \\ \mu = (4)/(5)`

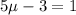
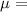`\mu =` 0.8 minutes