Question

N4M.6 A board has one end wedged under a rock having a mass of 380 kg and is supported by another rock that touches the bottom side of the board at a point 85 cm from the end under the rock. The board is 4.5 m long, has a mass of about 22 kg, and projects essentially horizontally out over a river. Is it safe for an adult with a mass of 62 kg to stand at the unsupported end of the board

Answer 1

it is safe to stand at the end of the table

Step-by-step explanation:

For this exercise we use the rotational equilibrium condition

Στ = 0

W x₁ - w x₂ - w_table x₃ = 0

M x₁ - m x₂ - m_table x₃ = 0

where the mass of the large rock is M = 380 kg and its distance to the pivot point x₁ = 850 cm = 0.85m

the mass of the man is 62 kg and the distance

x₂ = 4.5 - 0.85

x₂ = 3.65 m

the mass of the table (m_table = 22 kg) is at its geometric center

x_{cm} = L/2 = 2.25 m

x₃ = 2.25 -0.85

x₃ = 1.4 m

let's look for the maximum mass of man

m_{maximum} =
`( M x_1 -m_(table) x_3)/( x_2)`

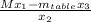
let's calculate

m_{maximum} =
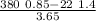`( 380 \ 0.85 - 22 \ 1.4)/(3.65)`(380 0.85 - 22 1.4) / 3.65

m_{maximum} = 80 kg

we can see that the maximum mass that the board supports without turning is greater than the mass of man

m_{maximum}> m

consequently it is safe to stand at the end of the table