Question

Stonewall receives ¢250 per year in simple interest from an amount of money he invested in

ADB, Barclays and GCB. Suppose ADB pays an interest of 2%, Barclays pays an interest of

4% and GCB pays an interest of 5% per annum and an amount of ¢350 more was invested in

Barclays than the amount invested in ADB and GCB combined. Also, the amount invested in

Barclays is 2 times the amount invested in GCB.

a) Write down the three linear equations and represent them in the matrix form AX = B.

b) Find the amount of money Stonewall invested in ADB, Barclays and GCB using Matrix

Inversion​

Answer 1

The amount invested in ADB is ¢1363.
`\overline 3` =

The amount invested in Barclays is ¢3,427.
`\overline 3`

The amount invested in GCB is ¢1,713.
`\overline 3`

Explanation:

The parameters of the investment Stonewall made are;

The amount in interest he receives from ADB, Barclays and GCB = ¢250

The amount of interest ADP pays = 2% per annum

The amount of interest Barclays pays = 4% per annum

The amount of interest GCB pays = 5% per annum

The amount invested in Barclays = The amount invested in ADB and GCB + ¢350

The amount invested in Barclays = 2 × The amount invested in GCB

a) Let 'x', represent the amount invested in ADB, 'y' represent the amount invested in Barclays, and 'z', represent the amount invested in GCB

We have;

y = x + z + 350

y = 2·z

0.02·x + 0.04·y + 0.05·z = 250

Therefore, we get the three linear equations as follows;

-x + y - z = 350...(1)

y - 2·z = 0...(2)

0.02·x + 0.04·y + 0.05·z = 250...(3)

Using Matrix inversion, we have;

`\left[\begin{array}{ccc}-1&1&-1\\0&1&-2\\0.02&0.04&0.05\end{array}\right] * \left[\begin{array}{c}x&y&z\end{array}\right] = \left[\begin{array}{c}350&0&250\end{array}\right]`

The transpose of the 3 by 3 matrix
`M^T` is given as follows;

`M^T = \left[\begin{array}{ccc}-1&0&0.02\\1&1&0.04\\-1&-2&0.05\end{array}\right]`

The Adjugate Matrix is given as follows;

`Adj = \left[\begin{array}{ccc}0.13&-0.09&-1\\-0.04&-0.03&-2\\-0.02&0.06&-1\end{array}\right]`

The inverse of the matrix = Adj/Det where, Det = -0.15, is therefore;

`M^(-1) = \left[\begin{array}{ccc}(-13)/(15) &(3)/(5) &(20)/(3) \\\\(4)/(15) &(1)/(5) &(40)/(3) \\\\(2)/(15) &-(2)/(5) &(20)/(3) \end{array}\right]`

We therefore, get the solution as follows;

`\left[\begin{array}{ccc}(-13)/(15) &(3)/(5) &(20)/(3) \\\\(4)/(15) &(1)/(5) &(40)/(3) \\\\(2)/(15) &-(2)/(5) &(20)/(3) \end{array}\right]* \left[\begin{array}{c}350&0&250\end{array}\right] = \left[\begin{array}{c}(4,090)/(3) \\&(10,280)/(3) \\ & (5,140)/(3) \end{array}\right]`

`\begin{array}{c}x = (4,090)/(3) \\&y = (10,280)/(3) \\ & z = (5,140)/(3) \end{array}`

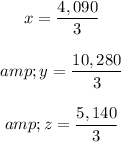
The amount invested in ADB, x = ¢4,090/3 = ¢1363.
`\overline 3`

The amount invested in Barclays, y = ¢10,282/3 = ¢3,427.
`\overline 3`

The amount invested in GCB, z = ¢5,140/3 = ¢1,713.
`\overline 3`