Answer:
A. The value of n can be any positive integer resulting in the same factor
Explanation:
Given
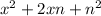 --- the right expression
--- the right expression
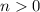
Required
Possible values of n
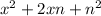
Expand
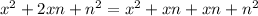
Factorize
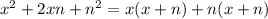
Factor out

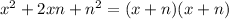
From the expression above, we can see that the result has the same factor. This means that options (b), (d) and (e) are not possible
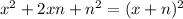
The above also shows that n can take any positive value.
Hence: (a) is correct