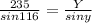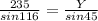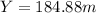Question

The Colonel spots a campfire at a bearing N 71 ∘ E from his current position. Sarge, who is positioned 235 feet due east of the Colonel reckons the bearing to the fire to be N 45 ∘ W from his current position. Determine the distance from the campfire to each man, rounded to the nearest foot.

Answer 1

`X=85.123m`

`Y=184.88m`

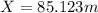
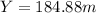
Explanation:

From the question we are told that:

Campfire Bearing from Colonel
`x=N 71 \textdegree E`

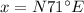
Distance b/w Colonel and Sarge
`Z=235feet`

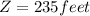
Campfire Bearing from Sarge
`y=N 45 \textdegree E`

Generally the angles x' and y' are solved

`x'=90 \textdegree-71 \textdegree`

`x'=19 \textdegree`

`y'=90 \textdegree-45 \textdegree`

`y'=45 \textdegree`

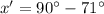
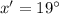
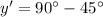
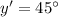
Generally the angle z' is solved

Sum of angles of a triangle is 180

Therefore

`z'=180 \textdegree-(19+45) \textdegree`

`z'=116 \textdegree`

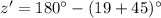
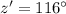
Generally the sine rule equation for for all distances is mathematically given by

`(Z)/(sinz')=(X)/(sinx')=(Y)/(siny)`

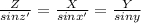
Generally the the distance b/w the Colonel and the campfire X is mathematically given as

`(235)/(sin116)=(X)/(sinx')`

`(235)/(sin116)=(X)/(sin19)`

`X=85.123m`

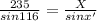
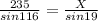
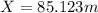
Generally the the distance b/w Sarge and the campfire X is mathematically given as

`(235)/(sin116)=(Y)/(siny)`

`(235)/(sin116)=(Y)/(sin45)`

`Y=184.88m`