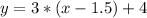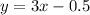Answer:
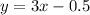
Explanation:
Given
Goes through
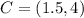
Parallel to AB
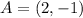
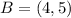
Required
Determine the line equation
First, calculate the slope of AB
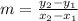
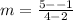
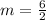
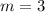
The line is said to be parallel to AB. This implies that their slopes are equal.
The equation of the line is then calculated as:

Where:
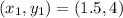
So: