Question

Two trains are 1.5 miles apart, train a is traveling at 3/4 the speed of train b if they meet in 4 minutes how fast is each train going

Answer 1

Train A is travelling at a speed of 12.857 miles per hour and train B at a speed of 9.643 miles per hour.

Explanation:

Let suppose that train A begins in position
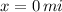`x = 0\,mi` and the train B in position
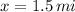`x = 1.5\,mi`, if
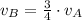`v_(B) = (3)/(4)\cdot v_(A)` and both trains move at constant speed, then we have the following kinematic equations:

Train A

`x_(A) = x_(A,o)+v_(A)\cdot t` (1)

Train B

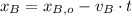`x_(B) = x_(B,o)-v_(B)\cdot t` (2)

If both trains meet each other, then
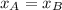`x_(A) = x_(B)`. If we know that
`x_(A,o) = 0\,mi`,
`x_(B,o) = 1.5\,mi`,
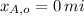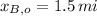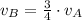`v_(B) = (3)/(4)\cdot v_(A)` and
`t = (1)/(15)\,h`, then we have the following expression:

`x_(A,o)+v_(A)\cdot t = x_(B,o)-v_(B)\cdot t`

`x_(A,o) + v_(A)\cdot t = x_(B,o) - (3)/(4)\cdot v_(A)\cdot t`

`(7)/(4)\cdot v_(A)\cdot t = x_(B,o)-x_(A,o)`

`v_(A) = (4\cdot (x_(B,o)-x_(A,o)))/(7\cdot t)`

`v_(A) = 12.857\,(mi)/(h)`

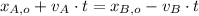
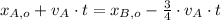
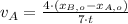
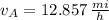
Then, the speed of the train B is:

`v_(B) = 9.643\,(mi)/(h)`

Train A is travelling at a speed of 12.857 miles per hour and train B at a speed of 9.643 miles per hour.