Question

g A report on the nightly news broadcast stated that 10 out of 108 households with pet dogs were burglarized and 20 out of 208 without pet dogs were burglarized. Suppose that this data is used to test the claim that the proportion of households with dogs that are burglarized is the same as the proportion of households without dogs that are burglarized. What would be the test statistic for this test

Answer 1

Test statistic |Z| = 0.1040 < 1.96 at 0.05 level of significance

Explanation:

Step(i):-

Given that a report on the nightly news broadcast stated that 10 out of 108 households with pet dogs were burglarized

First proportion

`p_(1) = (x_(1) )/(n_(1) ) = (10)/(108) = 0.0925`

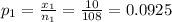
Given that a report on the nightly news broadcast stated that 20 out of 208 households without pet dogs were burglarized

Second proportion

`p_(2) = (x_(2) )/(n_(2) ) = (20)/(208) = 0.0961`

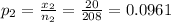
where

`P = (n_(1)p_(1) +n_(2)p_(2) )/(n_(1) +n_(2) )`

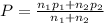
P = 0.09486

Q = 1 - P = 1 - 0.09486 = 0.90514

Step(ii):-

Test statistic

`Z = \frac{p_(1)-p_(2) }{\sqrt{PQ((1)/(n_(1) ) +(1)/(n_(2) ) )} }`

`Z = \frac{0.0925-0.0961 }{\sqrt{0.09486 X 0.90514((1)/(108 ) +(1)/(208 ) )} }`

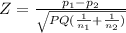
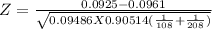
Z = -0.1040

|Z| = |-0.1040|

|Z| = 0.1040

Critical value Z = 1.96 at 0.05 level of significance