Question

The star Betelgeuse is 6.1 x 10^18 m away from Earth. How old is the light we see from that star when it reaches us? There are 3.2 x 10^7 seconds in a year (1 point)

635 years old

481 years old

727 years old

559 years old

Answer 1

635 years old

Step-by-step explanation:

The light reaching the earth from the sun will travel at a speed called the speed of light, and this has a universal value of 3 × 10⁸ m/s. Bearing this in mind, let us calculate the age of the light reaching the Earth from the sun:

Distance of star from Earth = 6.1 × 10⁸m

Speed of light = 3 × 10⁸ m/s

We have distance and speed, let us calculate the time of travel of the light from the star to the earth.

Distance = speed × time

6.1 × 10⁸ = 3 × 10⁸ × time

`time = (6.1 * 10^(18))/(3 * 10^8)`

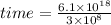
In order to do the division above, we will divide the whole numbers normally, then we will apply the law of indices to the power that says:

Xᵃ ÷ Xᵇ = X⁽ᵃ⁻ᵇ⁾

`\therefore time = (6.1 * 10^(18))/(3 * 10^8)\\= (2.03 * 10^((18-8)))/(1) \\= 2.03 * 10^(10)}\ seconds`

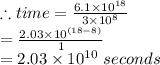
Next, we are told that there are 3.2 × 10⁷ seconds in a year.

∴ The number of years travelled by the light from the star:

`3.2\ * 10^7\ seconds = 1\ year\\1\ second = (1)/(3.2\ * 10^7) \\\therefore 2.03 * 10^(10)\ seconds = (2.03 * 10^(10))/(3.2\ * 10^7)`

please note that:

2.03 × 10¹⁰ = 20300000000

3.2 × 10⁷ = 32000000

`\therefore (2.03 * 10^(10))/(3.2\ * 10^7)\\= (20300000000)/(32000000) \\\\= (20300)/(32) \\= 634.347\ years\\`

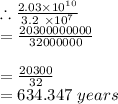
The closest answer in the option is 635 years, and we are short of this by some points due probably to approximations in the calculation.