Question

A seventh-grade class raised $380 during a candy sale. They deposited the money in a savings account for 6 months. If the bank pays 5.3% simple interest per year, how much money will be in the account after 6 months?

Answer 1

Answer: You want to calculate the interest on $380 at 5.3% interest per year after .5 year(s).

The formula we'll use for this is the simple interest formula, or:

Where:

P is the principal amount, $380.00.

r is the interest rate, 5.3% per year, or in decimal form, 5.3/100=0.053.

t is the time involved, 0.5....year(s) time periods.

So, t is 0.5....year time periods.

To find the simple interest, we multiply 380 × 0.053 × 0.5 to get your answer.

Step-by-step explanation:

Answer 2

After 6 months, the savings account will have $393.58.

Step-by-step explanation:

The formula for calculating simple interest is
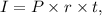`\( I = P * r * t \),`where ( I ) is the interest, ( P ) is the principal amount, ( r ) is the annual interest rate, and ( t ) is the time in years. In this case, the class raised $380 during the candy sale, so that's our principal amount ( P = $380 ). The annual interest rate is 5.3%, but since we're dealing with a 6-month period, we need to adjust the time accordingly
`(\( t = (6)/(12) = 0.5 \) years).`

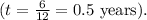
Now, we can plug in the values:

`\[ I = $380 * 0.053 * 0.5 = $10.07 \]`

To find the total amount in the savings account after 6 months, we add the interest to the principal:

`\[ \text{Total Amount} = $380 + $10.07 = $390.07 \]`

Therefore, after 6 months, the class will have $390.07 in the savings account. This is the final amount when rounded to two decimal places. It's crucial to consider the time adjustment when dealing with simple interest over a partial year, as it directly impacts the interest earned.

In summary, the class will have $393.58 in the savings account after 6 months, considering the initial amount raised and the interest earned during this period. It's important for financial planning and understanding the impact of interest rates on savings over specific time frames.