Question

A baseball is hit and its height is given by h = 29.4t – 4. 9t^2, where h is the

height of the ball in metres and t is time in seconds. Determine the maximum height
of the baseball.

Answer 1

44.1m

Explanation:

we are given a quadratic function which represents the height and time of a baseball

`\displaystyle h = 29.4t - 4.9 {t}^(2)`

we want to figure out maximum height of

the baseball

since the given function is a quadratic function so we have a parabola

which means figuring out the maximum height is the same thing as figuring out the maximum y coordinate (vertex)

to do so we can use some special formulas

recall that,

`\displaystyle \rm t= ( - b)/( 2a)`

`\displaystyle H_{\text{max}}=f(t)`

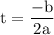
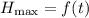
notice that, our given function is not in standard form i.e

`\displaystyle f(x) = a {x}^(2) + bx + c`

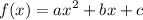
let's make it so

`\displaystyle h = - 4.9 {t}^(2) + 29.4t`

therefore we got

our a is -4.9 and b is 29.4

so substitute:

`\displaystyle\rm t= ( -( 29.4))/( 2 \cdot - 4.9)`

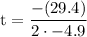
remove parentheses and change its sign:

`\displaystyle\rm t= ( -29.4)/( 2 \cdot - 4.9)`

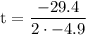
simplify multiplication:

`\displaystyle\rm t= ( -29.4)/( - 9.8)`

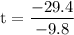
simplify division:

`\displaystyle \: t = 3`

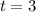
so we have figured out the time when the baseball will reach the maximum height

now we have to figure out the height

to do so

substitute the got value of time to our given function

`\displaystyle H_{\text{max}}=29.4\cdot 3-4.9\cdot {3}^2`

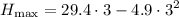
simplify square:

`\displaystyle H_{\text{max}}=29.4\cdot 3-4.9\cdot 9`

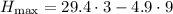
simplify mutilation:

`\displaystyle H_{\text{max}}=88.2-44.1`

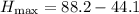
simplify substraction:

`\displaystyle H_{\text{max}}=44.1`

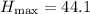
hence,

the maximum height of the baseball is 44.1 metres

Answer 2

Solution given:

height

h=29.4t – 4.9t²

differentiating each term with respect to time (t)

`(d'(h))/(d(t))`=
`(d(29.4t – 4.9t²))/(d(t))`

`(d'(h))/(d'(t))`=29.4-9.8t

again second derivative

`(d''(h))/(d`=-9.8

for maximum, minimum

first derivative =0

29.4-9.8t=0

t=
`(29.4)/(9.8)`=3

So it attains maximum height at t=3

so

maximum height=29.4×3-4.9×3² =44.1meters

So.

maximum height of the basketball is 44.1meters