Answer:
tee shirt:4
sleeve shirt:3
Explanation:
we are given two conditions
- Matt bought 7 shirts for a total of $38
- Tee shirts cost 5 dollars and long sleeve shirts cost 6 dollars
we want to figure out how many each type of shirt he bought
let tee and sleeve shirts be t and s respectively
according to the first condition
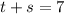
according to the second condition
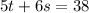
therefore
our system of linear equation is
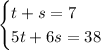
so
now we need our algebra skills to figure out t and s
to do so we can use substitution method
cancel s from both sides of the first equation:

now substitute the value of i equation to the second equation:
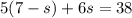
distribute:
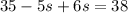
collect like terms:
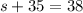
cancel 35 to both sides:
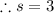
now substitute the value of s to the i equation:
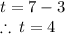
hence,
he bought tee shirt 4 and sleeve shirt 3