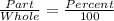Question

Which proportion correctly shows the relationship between the part, whole, and percent of a percent problem

Answer 1

C.
`(Part)/(Whole) =(Percent)/(100)`

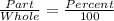
Explanation:

A good way to think about it is this. You know that 1/2 is 50%. It's common knowledge.

In this case 1 is the Part and 2 is the whole

`(Part)/(Whole) = (1)/(2) = .50`

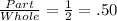
So to get 50% in decimal form we would have to divide it by 100 to move the decimal over two places

`(Percent)/(100) = (50)/(100) = .50`

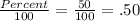
Therfore,

`(1)/(2) = (50)/(100)`

or

`(Part)/(Whole) =(Percent)/(100)`