Question

I need help on this math problem fast with work shown and answer thx

Answer 1

angle 1 = 124

angle 2 = 56

angle 3 = 124

angle 4 = 56

Explanation:

This problem is a bit like a puzzle. To make notation easier I'm going to do this:

angle 1 = a

angle 2 = b

angle 3 = c

angle 4 = d

Now, let's start with what we know from the image.

All angles added together form a circle or 360 degrees

a + b + c + d = 360

In the same regard a + d = 180, and b + c = 180

Also,

a = c

and

b = d

It also tells us angle 4 is 25 degrees greater than one fourth of angle 1. Which is written as.

d = 1/4(a) + 25

If we look at all the equations we have, we can see that two of the equations have two of the same variables:

a + d = 180

and

d = 1/4(a) + 25

Using substitution we can take the second equation substitute it for d in the first equation giving us:

a + (1/4(a) + 25) = 180

Now we just solve for a

`(4)/(4) a+ (1)/(4) a + 25 = 180\\\\(5)/(4)a + 25 = 180 \\\\((5)/(4)a + 25) - 25 = (180) -25\\\\(5)/(4) a = 155\\\\(5)/(4) a * (4)/(5) = 155 * (4)/(5)\\\\a = 124`

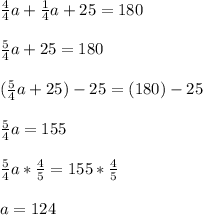
Therefore a, or angle 1, is 124

Since a = c, then c, or angle 3, is also 124

Since a + d = 180 and a = 124 then

d = 180 -124

d = 56

So, d, or angle 4, is 56

And because b = d then b, or angle 2, is also 56

a = 124

b = 56

c = 124

d = 56

For extra measure, we can check our work by using the first equation

a + b + c + d = 360

124 + 56 + 124 + 56 = 360