Answer:
![\displaystyle y' = (-2)/(x \ln (10)[\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/2tvff7j8hgcdoju90pm5232vpuw0hr17bf.png)
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2023/formulas/mathematics/college/n4n2zkyxd59vf56w6umbi199ixab4hs43u.png)
Derivative Rule [Basic Power Rule]:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2023/formulas/mathematics/college/jtcp2pka45ti9vmszt8xaivl7kkebnrtlp.png)
Explanation:
Step 1: Define
Identify.
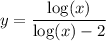
Step 2: Differentiate
- [Function] Derivative Rule [Quotient Rule]:
![\displaystyle y' = ([\log (x) - 2][\log (x)]' - [\log (x) - 2]'[\log (x)])/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/ex72d8o7ocwknc0afnfpakfy8t7pcfebyi.png)
- Rewrite [Derivative Rule - Addition/Subtraction]:
![\displaystyle y' = ([\log (x) - 2][\log (x)]' - [\log (x)' - 2'][\log (x)])/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/wyihay9d35goqzb9u1j5n0r2pbcd24omg6.png)
- Logarithmic Differentiation:
/(\ln (10)x) - [(1)/(\ln (10)x) - 2'][\log (x)])/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/fn27091f2qlua4hzvzsjod4k2mly8hhnxh.png)
- Derivative Rule [Basic Power Rule]:
/(\ln (10)x) - (1)/(\ln (10)x)[\log (x)])/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/bu7nnxa2jyaqfx8mmfclhz83ra8h1hknpn.png)
- Simplify:
![\displaystyle y' = ((\log (x) - 2)/(\ln (10)x) - (\log (x))/(\ln (10)x))/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/uwtmfctmat648b17n1vhxvxugzgomlw2pv.png)
- Simplify:
![\displaystyle y' = ((-2)/(\ln (10)x))/([\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/8xvqee91jpd91u1j8gjm3fmhm78lr3lzgp.png)
- Rewrite:
![\displaystyle y' = (-2)/(x \ln (10)[\log (x) - 2]^2)](https://img.qammunity.org/2023/formulas/mathematics/college/2tvff7j8hgcdoju90pm5232vpuw0hr17bf.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation