Question

Use the inequalities to answer the following question

Inequality 1: 2x + 7 < -3
Inequality 2: x – 8 + 3x < -4
Which of the following values make both inequalities TRUE? Select all that apply.

A.) 12

B.) 325

C.) –10

D.) 2/3

E.) –8.25

F.) -15/2

G.)–5

Answer 1

C, E, and F

Step-by-step explanation:

There are two ways to answer this question. First, you could simply input each answer into both equations to see which one works but that would take quite a long time.

A better way is to simply solve each equation for x.

You could rewrite

2x + 7 < -3

as

2x + 7 = -3

and solve:

Subtract 7 from both sides

`(2x + 7) -7 = (-3) - 7\\2x = -10`

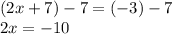
Now divide both sides by 2

`(2x)/(2) = (-10)/(2)\\x = -5`

Now we can simply replace the equals sign with the inequality

x < -5

Where you can run into trouble is if you have to multiply or divide by a negative number across the equation, you must flip the inequality sign. It's best to leave it there to remind you, but I switched it out just to show that it's no different than a typical algebraic equation.

Now, we know that x can be any value less than -5. Let's find out the same thing for the second equation:

`x - 8 + 3x < -4\\(x + 3x) -8 < -4\\4x - 8 < -4\\(4x - 8) + 8 < (-4) + 8\\4x < 4\\(4x)/(4) < (4)/(4)\\x < 1`

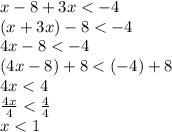
Now we know that x must be less than 1 for the second equation. So, now we can choose the answers that are both less than -5 and less than 1.

These answers are:

C. -10

E. -8.24

and

F. -15/2 which is -7.5

NOTE: -5 is equal to but not less than -5 so G is not included.