Answer:
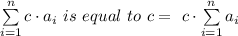
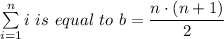
![\sum\limits_(i=1)^(n) i^3 \ is \ equal \ to \ e = \left [ (n \cdot (n + 1))/(2) \right]^2](https://img.qammunity.org/2022/formulas/mathematics/high-school/a5p4tnnxvamtb11at4ok20off0z0cj871l.png)
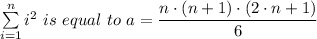
Explanation:
1) The sum of a series of the cubes of numbers 'i' is given as follows;
Sₙ = n/2 × (1st term + Last term)
∴ Sₙ = n/2 × (1 + n) = n·(n + 1)/2
It can be shown that the sum of a series of the cubes of numbers 'i²' is given as follows;
Sₙ = (n·(n + 1)·(2·n + 1))/6
It can be also be shown that the sum of a series of the cubes of numbers 'i³' is given as follows;
Sₙ = (n·(n + 1)/2)²
Therefore, we have;
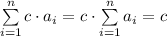

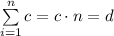
![\sum\limits_(i=1)^(n) i^3 = \left [ (n \cdot (n + 1))/(2) \right]^2 = e](https://img.qammunity.org/2022/formulas/mathematics/high-school/i3o7fnvbr3clktn4hmu0abd76u4v987fx8.png)
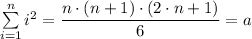 .
.