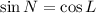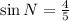Answer:
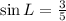
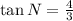
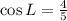
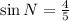
Explanation:
Given
The above triangle
First, we calculate the length LM using Pythagoras theorem.
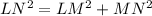
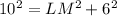
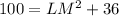
Collect like terms
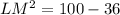
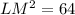
Take positive square root
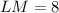
Solving (a): Sin L
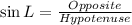
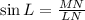
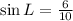
Simplify
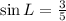
Solving (b): tan N
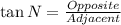
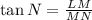
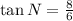
Simplify
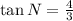
Solving (c): cos L
This calculated as:
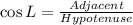
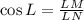
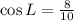
Simplify
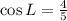
Solving (d): sin N
This is calculated using:
If
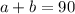
Then:
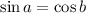
So: