Answer:
The hourly growth rate parameter is of 4.74%
Explanation:
Continuous growth model:
The continuous growth model for a population after t hours is given by:
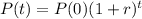
In which P(0) is the initial population and r is the hourly growth rate parameter, as a decimal.
A sample of 1500 bacteria selected from this population reached the size of 1805 bacteria in four hours.
This means that
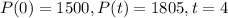
Find the hourly growth rate parameter.
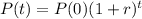

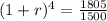
![\sqrt[4]{(1+r)^4} = \sqrt[4]{(1805)/(1500)}](https://img.qammunity.org/2022/formulas/mathematics/college/7z3qv1fw0xh38boflb9fg1gppnf8ofxxuo.png)
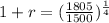


0.0474*100% = 4.74%
The hourly growth rate parameter is of 4.74%